Most of my work in the past year has been boundary surveying, requiring me to take the Triumph-LS into some pretty difficult places with phenomenal success. However, in these places precision is diminished by multipath. For my purposes the reduced precision is still tolerable and in most cases on large boundaries is still better than (and acquired much faster than) conventional terrestrial traversing.
Because my work has mostly consisted of pushing the LS in hostile environments, I forget sometimes just how good the Triumph-LS is in good environments with open skies. Last week I was hired to create five control points on a large site for machine control. I worked from two existing control points (Point 5 and Point 553). I set the base directly on 5 and tied into 553 as a check. Point 5 was established in 2003 and Point 553 was established from it in 2006 using static GPS. Both are 12" spikes in stable soil. My new points are 1/2" x 24" rebar. I tied point 553 only once (I had intended to tie in twice, but forgot to return to it). I tied my new points twice each except for 13 which I tied three times.
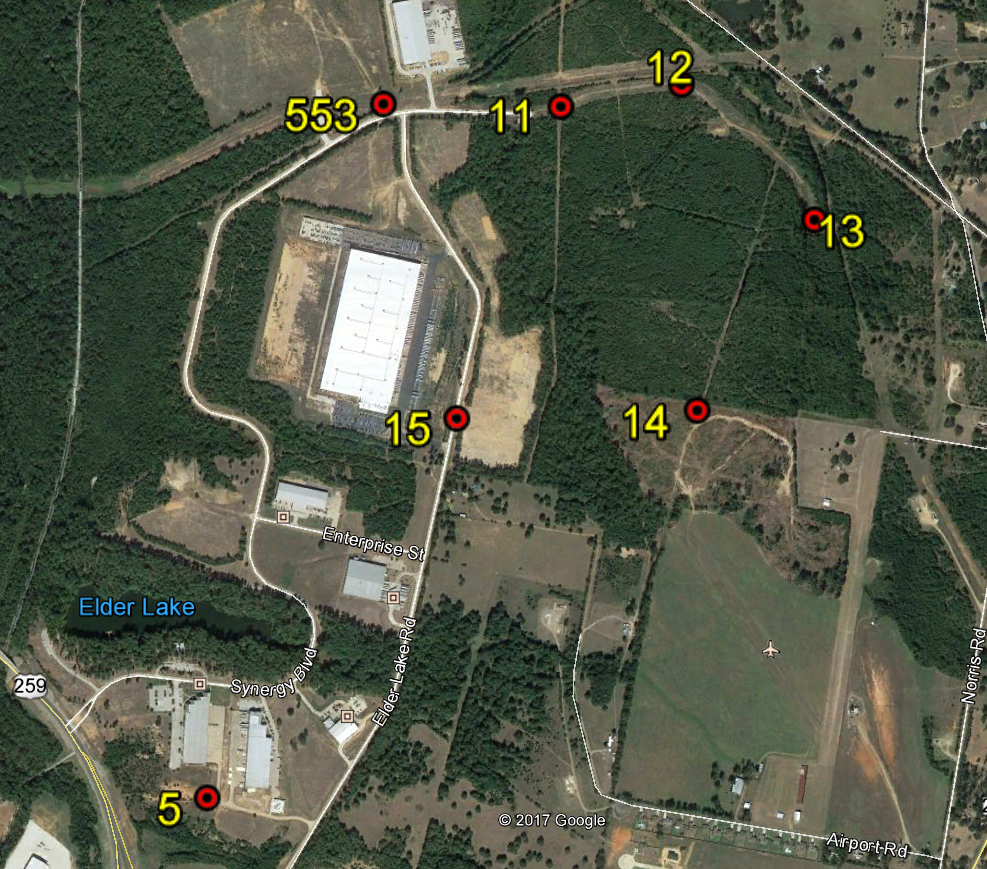
Because my work has mostly consisted of pushing the LS in hostile environments, I forget sometimes just how good the Triumph-LS is in good environments with open skies. Last week I was hired to create five control points on a large site for machine control. I worked from two existing control points (Point 5 and Point 553). I set the base directly on 5 and tied into 553 as a check. Point 5 was established in 2003 and Point 553 was established from it in 2006 using static GPS. Both are 12" spikes in stable soil. My new points are 1/2" x 24" rebar. I tied point 553 only once (I had intended to tie in twice, but forgot to return to it). I tied my new points twice each except for 13 which I tied three times.